Categoriearchief: wiskunde

Gewicht – gewichten omrekenen: gram, kilo, pond, ons, ton, kg, hg, dag, g, dg, cg, mg

Gewichten omrekenen: uitleg video

Gewichten omrekenen, gram, ons, kg, pond, enz.: oefenen met werkbladen en/of leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§14 en §15 van het leerwerkboek)
14_1
14_2
14_3
14_4
14_5

 

15_1
15_2
15_3
15_4
15_5

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §14 en §15 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Uitleg eerste deel, samenvatting

kilo: duizend
hecto: honderd
deca: tien
deci: een tiende
centi: een honderdste
milli: een duizendste
 Naast kilogram gebruik je bij gewichten ook weer alle andere bekende voorvoegsels die je al leerde bij de paragraaf over het omrekenen van lengtematen.
1 kg = 1000 g
1 hg = 100 g
1 dag = 10 g
1 g
1 dg = 0,1 g
1 cg = 0,01 g
1 mg = 0,001 g

kg | hg | dag | g | dg | cg | mg
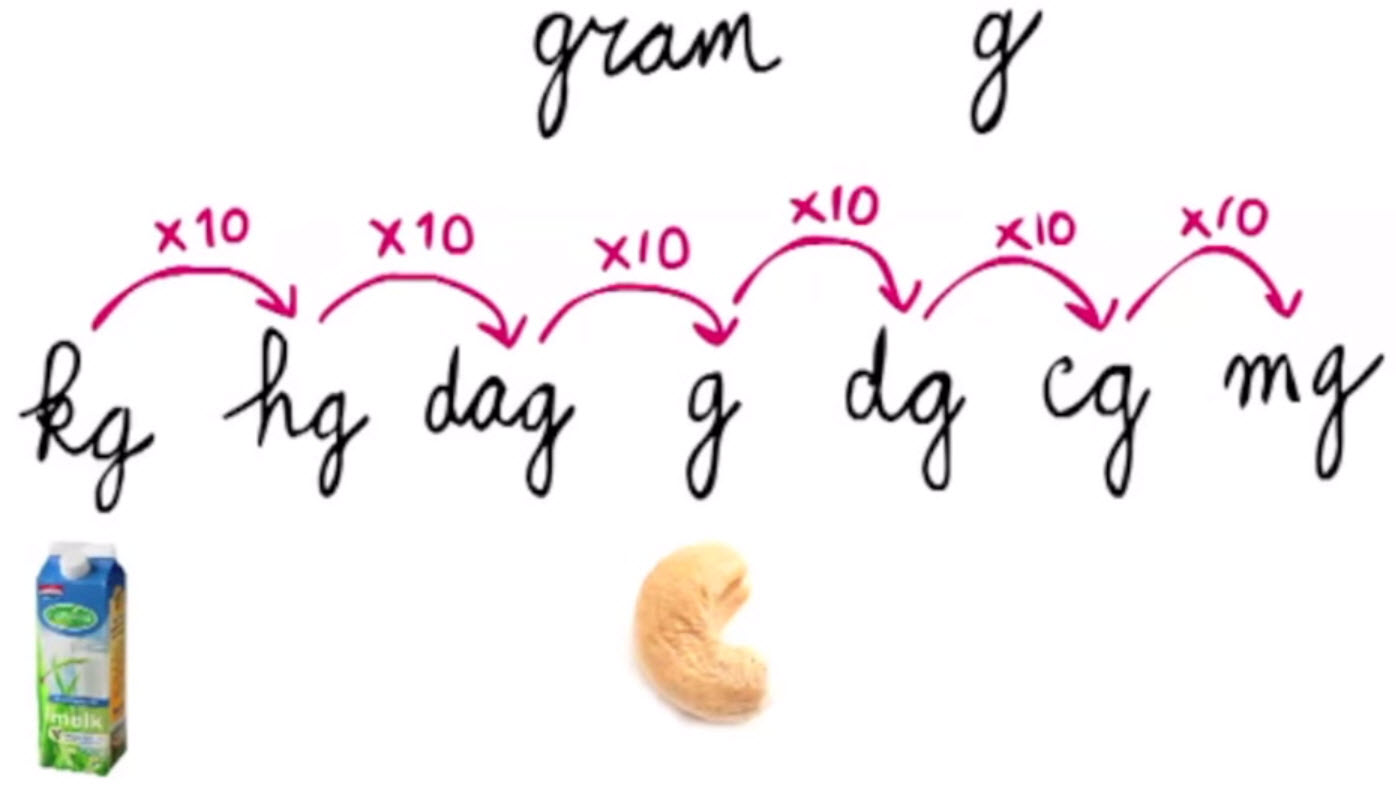gewichtmaten omrekenen Het omrekenen van gewichtmaten gaat op dezelfde manier als het omrekenen van lengtematen.Je kijkt eerst hoe groot de ‘afstand’ is tussen de twee eenheden. Daarna kijk je of de komma naar rechts of naar links moet.

De komma één plaats naar rechts betekent vermenigvuldigen met 10.
Als je dit niet meer begrijpt, kun je nog even de paragraaf over kommagetallen vermenigvuldigen met 10, 100, enz. herhalen en de paragraaf over kommagetallen delen door 10, 100, enz.

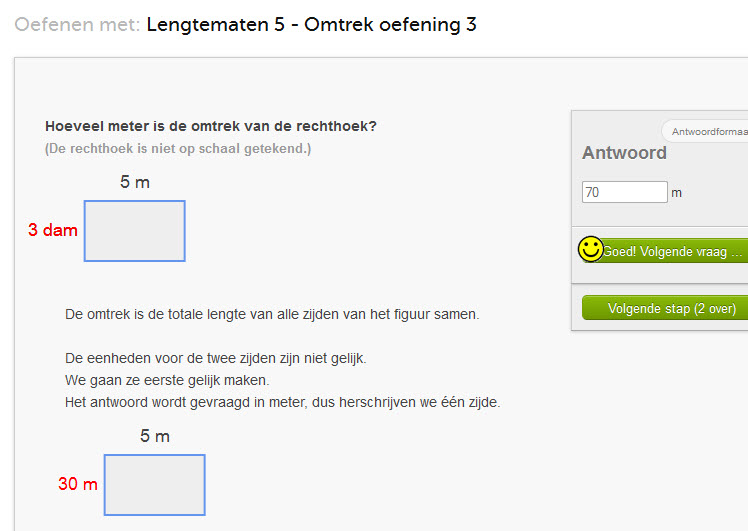
Gewichten omrekenen zoals kilogram, gram, centigram, milligram: online oefenen

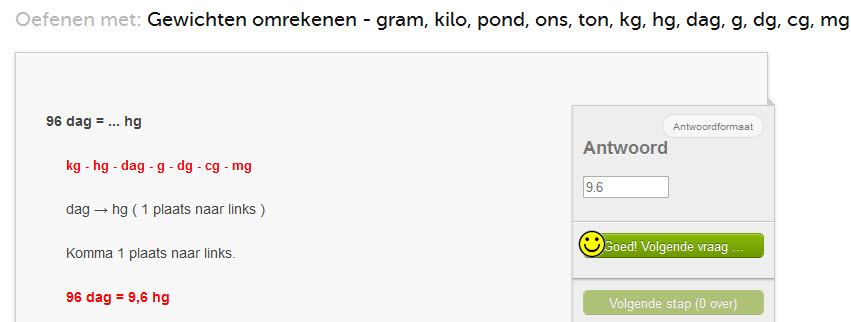
Oefenen met het omrekenen van gewichtseenheden: kg, hg, dag, g, dg, cg, mg

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


gewicht

Uitleg tweede deel, samenvatting

We bekijken in deze paragraaf de gewichtseenheden die veel worden gebruikt in het dagelijks leven.

omrekenen gewicht Gewichten meet je in gram.

gram

Je ziet hier een cashew nootje van ongeveer één gram.
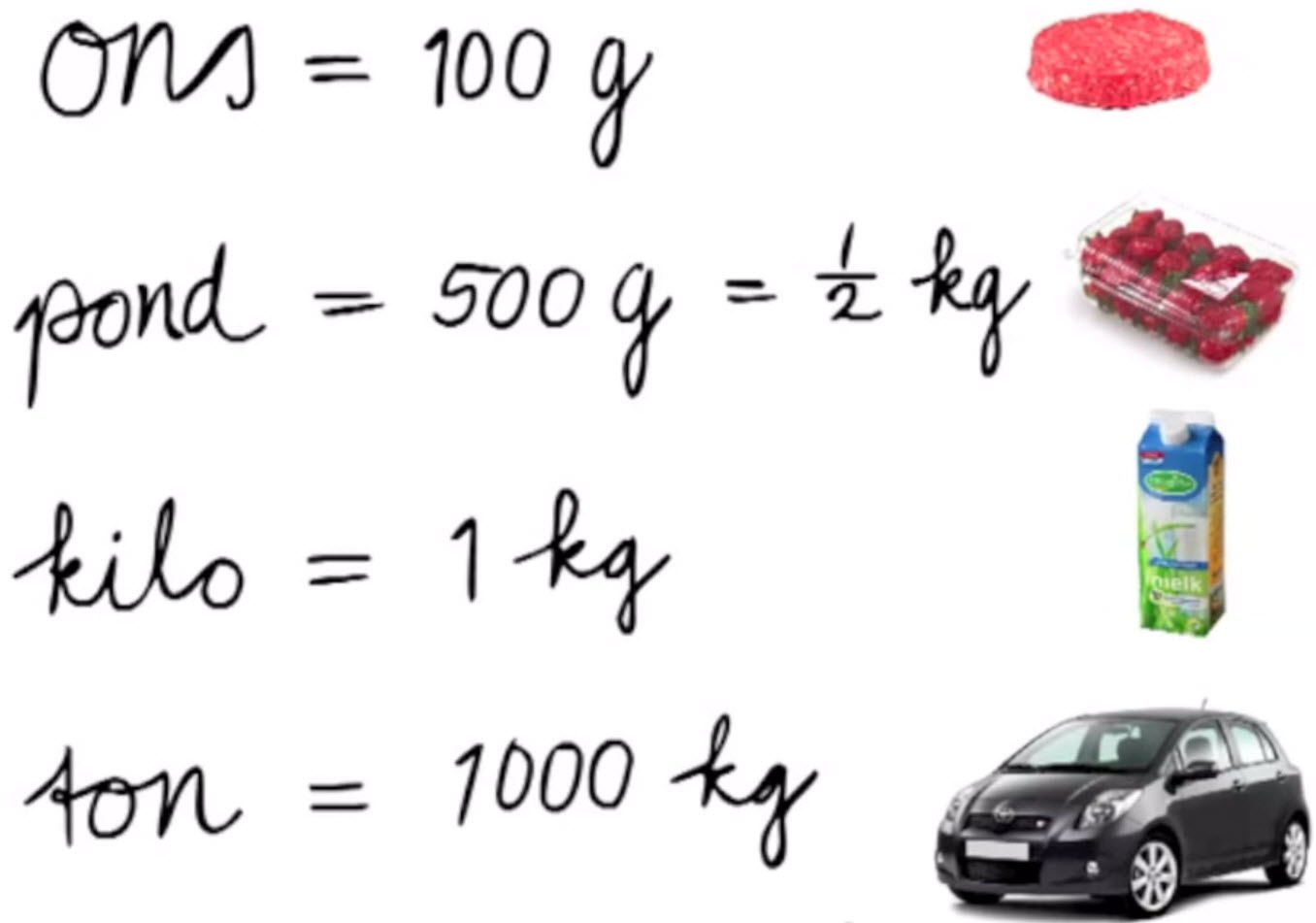omrekenen gewicht Hier zie je een paar voorbeelden van voorwerpen van ongeveer een ons, pond, kilo en ton.
gewicht
ons = 100 gram = 1/10 kilogram

24 kleine suikerklontjes wegen samen ongeveer één ons.
gewicht pondEen pak bonen weegt ongeveer één pond.
pond = 500 gram = 1/2 kilogram
gewicht
kilo (of kilogram) = 1000 gram

Een liter vloeistof weegt ongeveer één kilogram.

1 kilo = 2 pond = 10 ons = 1000 gram
omrekenen gewichten
ton = 1000 kilogram

Een paard weegt ongeveer 1 ton.

Een gewone auto weegt ook ongeveer 1 ton.

Het gewicht van een vrachtauto is meestal 8 tot 10 ton.

Een gewone stadsbus weegt ongeveer 12 ton.
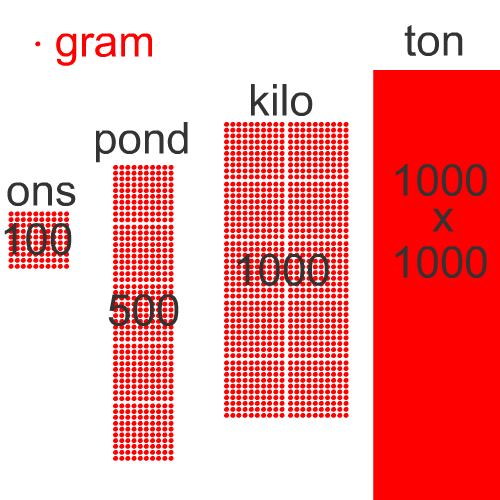omrekenen gewichten Hiernaast is een gram getekend als één rood stipje.
Je ziet dan dat een ons 100 gram is.
Een pond is 5 keer een ons, dus 500 gram.
Een kilo is 10 keer een ons, dus 1000 gram.
Een ton is gelijk aan duizend kilo.

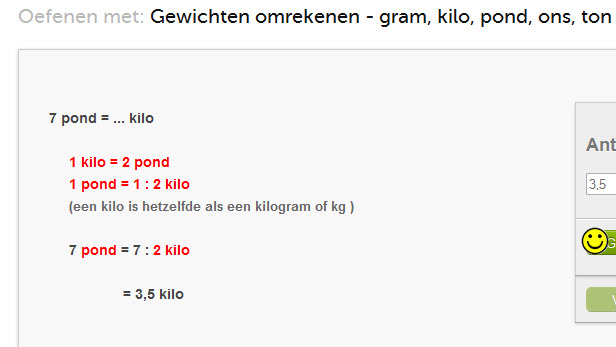
Gewichten omrekenen zoals gram, kilo, pond, ons, ton: online oefenen

Oefenen met het omrekenen van gewichtseenheden: gram, pond, ons, kilo, ton

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


inhoudsmaten-liter


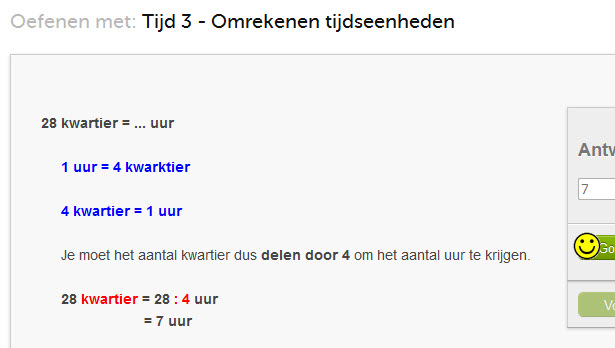
Gewichten omrekenen zoals kilo, pond, hectogram, decagram, enz.: online oefenen

Oefenen met het omrekenen van gewichtseenheden: pond, ons, kilo, ton, kg, hg, dag, g, dg, cg, mg

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


inhoudsmaten-liter

 

Tijd 3 – Omrekenen tijdseenheden

Geef een reactie

Uitleg video over omrekenen uur naar minuten enz.

Tijdseenheden omrekenen: oefenen met leerwerkboek

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof snel onder de knie krijgen als je oefent met §17 t/m §21 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Tijdseenheden omrekenen: oefenen met werkbladen

Oefen direct met de uitgelegde stof.
Dit kun je doen met het leerwerkboek en/of met onderstaande extra werkbladen met antwoordbladen.
Deze in totaal 25 werkbladen horen bij de paragrafen 17 t/m 21 uit het leerwerkboek.

§ titel .pdf .pdf .pdf .pdf .pdf
§ 19 Tijdseenheden omrekenen: seconden en minuten 19_1 19_2 19_3 19_4 19_5
§ 20 Tijdseenheden omrekenen: weken en maanden 20_1 20_2 20_3 20_4 20_5
§ 21 Tijdseenheden omrekenen: dagen en weken 21_1 21_2 21_3 21_4 21_5
§ 17 Tijdseenheden omrekenen: seconde, minuut, kwartier, uur 17_1 17_2 17_3 17_4 17_5
§ 18 Tijdseenheden omrekenen: dag, week, maand, jaar 18_1 18_2 18_3 18_4 18_5

 

Tijdseenheden omrekenen, bijv. kwartieren naar minuten: online oefenen

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


omrekenen uur naar minuten
omrekenen uur naar minuten
Klik op bovenstaand plaatje voor een printbare pdf met de tijdsgegevens.

Tijdseenheden: samenvatting

Tijd meet je in seconde.

seconde

Omdat een seconde erg kort is, gebruiken we veel meer eenheden in het dagelijks leven.

minuut = 60 seconde
kwartier = 15 minuten
uur = 60 minuten
dag (etmaal) = 24 uur
week = 7 dagen
maand = 28, 29, 30 of 31 dagen
jaar = 365 of 366 dagen

       = 52 weken en één of twee dagen

decennium = 10 jaar
eeuw = 100 jaar

 

 

Tijd 2 – Klokkijken, digitale klok

Geef een reactie

Digitale klok: uitleg video

Digitale klok: oefenen met werkbladen en/of leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§16 van het leerwerkboek)
16A_1
16A_2
16A_3
16A_4
16A_5

 

16B_1
16B_2
16B_3
16B_4
16B_5

 

16C_1
16C_2
16C_3
16C_4
16C_5

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §16 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Twee werkbladen over digitaal klokkijken.

Klik op een plaatje voor het openen van een werkblad met antwoordenblad.
De pdf wordt geopend in een nieuw tabblad.

digitale tijd op analoge klok: wijzers tekenen

digitale tijd op analoge klok: wijzers tekenen

digitaal klokrekenen, eerder en later

digitaal klokrekenen ,eerder en later

 

Digitale klok. Welk dagdeel is het, ochtend, middag, avond of nacht?: online oefenen

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


hele uren

Digitale tijd omzetten in analoge tijd: online oefenen

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


hele uren

Digitale tijd omzetten in analoge tijd; ook dagdeel benoemen: online oefenen

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


hele uren

Digitale klok: samenvatting

Een digitale klok heeft geen wijzers.
Je ziet bijvoorbeeld op de klok:

05:08

Dit betekent dat het 8 over 5 is. Het is dan nog heel vroeg in de ochtend.
Je kunt ook zien:

17:08

Dit betekent ook dat het 8 over 5 is, maar dan in de middag.

Een digitale klok begint bij 00:00 (dit is midden in de nacht, om 12 uur).
De klok eindigt bij 13.59 (dit is één minuut voor 12 in de nacht).

Tijd 1 – Klokkijken, analoge klok (wijzerklok)

Geef een reactie

Klokkijken met een analoge klok (wijzerklok): uitleg video

Onderstaande video kan het beste in stukjes worden bekeken. Eerst moet een kind de hele uren kunnen benoemen en daarmee oefenen voordat het aan de halve uren toe is, enz.
Daarom staat hieronder een lijstje met de punten waarop de video gestopt kan worden voor een bepaald onderdeel.

start stop onderwerp
0 1.46 Hoe lopen de wijzers?
1.46 3.40 hele uren
3.40 5.48 halve uren
5.48 8.55 kwart over of kwart voor
8.55 13.10 5 of 10 minuten voor of over het hele of halve uur
13.10 14.54 op de minuut exact
14.54 18.30 zelf tekenen van de wijzers
18.30 22 Vragen zoals: Hoe laat is het over drie kwartier?

Digitale klok: oefenen met leerwerkboek

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof snel onder de knie krijgen als je oefent met §17 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Hoe lopen de wijzers? Analoge klok: oefenen met werkbladen en online oefenen.

Hele uren

Halve uren

Hele en halve uren

kwart over en kwart voor; kwartier

vijf over (half) … | tien voor (half) …

Op de minuut exact

Hier onder een overzicht van alle werkbladen over de analoge klok.

Klik op een plaatje voor het openen van een werkblad met antwoordenblad.
De pdf wordt geopend in een nieuw tabblad.

1 | Hele uren

2 | Halve uren
klokkijken hele uren klokkijken halve uren

3 | Hele en halve uren

4 | Hele en halve uren
klokkijken hele uren klokkijken halve en halve uren wijzers tekenen

5 | Hele en halve uren

6 | Hele en halve uren, een uur later tekenen
klokkijken hele uren klokkijken halve en halve uren wijzers tekenen

7 | Hele en halve uren, een uur eerder tekenen

8 | Hele en halve uren, een half uur later tekenen
klokkijken hele uren klokkijken halve en halve uren wijzers tekenen

9 | Hele en halve uren, een half uur eerder tekenen

10 |Kwart voor en kwart over
klokkijken hele uren klokkijken halve en halve uren wijzers tekenen

11 | Over drie kwartier

12 | Drie kwartier geleden
klokkijken hele uren klokkijken halve en halve uren wijzers tekenen

13 | Vijf over, vijf voor, tien over, tien voor

14 | Op de minuut exact
klokkijken hele uren klokkijken halve en halve uren wijzers tekenen

Kloksjablonen voor docenten
klokkijken hele uren

Digitale klok: oefenen met leerwerkboek

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof snel onder de knie krijgen als je oefent met §17 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

 

Cito-toets tips en leeswijzer voor Cito rekensommen

1 reactie

Cito-toets tips rekenen: video uitleg

.
cito oefenen groep-7-8-plaatje Bij deze paragraaf hoort het leerwerkboek: Toets voorbereiding voor groep 7 en 8.
De Cito-score kan fors omhoog door dit doelgerichte oefenboek met antwoordenboek.

Bekijk de verkrijgbare titels op de winkelsite.
wiskunde piramide In dit leerwerkboek worden de eerste zes bouwlagen van de wiskunde-piramide behandeld.

Het rekenonderwijs/wiskundeonderwijs is opgebouwd als een piramide: elke laag bouwstenen wordt zorgvuldig op de vorige gelegd; je kunt geen laagje missen.

Slechts één slechte leer-periode kan er de oorzaak van zijn dat een leerling een reken-bouwlaag mist waardoor hij of zij misschien zelfs nooit meer iets van wiskunde zal begrijpen.

Met deze leerwerkboeken worden hiaten in kennis voorkomen.
Ook kunnen ontbrekende kennislagen achteraf worden opgevuld.

Klik hier voor meer informatie over het belang van een leerwerkboek.

Cito tips: samenvatting

Hier onder zie je cito-toets tips voor het lezen van een rekentoets-vraag van Cito.
Printbaar pdf met de cito-toets tips voor het lezen van een Cito vraag (opent in nieuwe tab).

  1. Schrijf de gegevens zo kort mogelijk op.
  2. Schrijf de kale som op.
  3. Bereken de kale som op een blaadje.
  4. Controleer je antwoord.

  1. Tips bij het kort opschrijven van de gegevens.
    • Kijk of je het plaatje nodig hebt.
      Soms staat er een belangrijk gegeven in de tekening maar soms ook niet.
    • Schrijf alle nodige gegevens van de tekening en van de tekst op een blaadje.
      Je hoeft daarna niet meer naar de tekening en naar de vraag te kijken.
    • Kijk goed of het woordje ongeveer in de vraag óf bij de mogelijke antwoorden staat.
      Zo ja, schrijf dit dan ook op je blaadje.
  2. Tips bij het opschrijven van de kale som.
    • Staat er ongeveer in de tekst of in de antwoorden?
      In dat geval moet je de getallen in de kale som meteen afronden!
    • Staat er bijvoorbeeld 1 op de 4, schrijf dat dan als 1 : 4 of als de breuk 1/4
    • Staat er bijvoorbeeld 2 van de 3, schrijf dat dan als 2 : 3 of als de breuk 2/3
  3. Tips bij het berekenen van de kale som.
    • Kun je de som gewoon snel uirekenen? Doe dat dan.
    • Ziet de som er te moeilijk uit of is het te veel rekenwerk? Maak dan een schatting van het antwoord.
      Heel vaak zie je meteen dat een of twee van de mogelijke antwoorden echt fout zijn. Maar kijk wel eerst of je het woordje ongeveer niet over het hoofd hebt gezien want de kale sommen zijn zelden te moeilijk.
    • Als je er niet uit komt, kun je ook op de plaats van de puntjes een van vier de mogelijke antwoorden zetten en kijken of alles dan klopt.
  4. Tips bij het controleren van het antwoord.
    • Vul je antwoord in de kale som in en kijk of het klopt.

 

Cito vragen over het metrieke stelsel

Geef een reactie
.
cito oefenen groep-7-8-plaatje Bij deze paragraaf hoort het leerwerkboek: Toets voorbereiding voor groep 7 en 8.
De Cito-score kan fors omhoog door dit doelgerichte oefenboek met antwoordenboek.

Bekijk de verkrijgbare titels op de winkelsite.
wiskunde piramide In dit leerwerkboek worden de eerste zes bouwlagen van de wiskunde-piramide behandeld.

Het rekenonderwijs/wiskundeonderwijs is opgebouwd als een piramide: elke laag bouwstenen wordt zorgvuldig op de vorige gelegd; je kunt geen laagje missen.

Slechts één slechte leer-periode kan er de oorzaak van zijn dat een leerling een reken-bouwlaag mist waardoor hij of zij misschien zelfs nooit meer iets van wiskunde zal begrijpen.

Met deze leerwerkboeken worden hiaten in kennis voorkomen.
Ook kunnen ontbrekende kennislagen achteraf worden opgevuld.

Klik hier voor meer informatie over het belang van een leerwerkboek.

Cito oefenen met het metrieke stelsel: uitleg video

Cito oefenen met het metrieke stelsel: samenvatting

In het witte en gele kader volg je de normale procedure.
In het donker blauwe kader zie je hoe je de vraag zonder echt te rekenen kunt beantwoorden.

cito oefenen
  1. 1 kilo kost 5 euro
    100 gram kost … euro
  2. 1 kilo kost 5 euro
    100 gram kost … euro
  3. 1 kilo kost 5 euro
    1000 gram kost 5 euro
    100 gram kost 0,5 euro
In de vraag zit het cijfer 5 en in één van de antwoorden ook.
Bovendien is C veel te duur voor één perzik.
cito oefenen groep 8
  1. 1,8 … is ongeveer 2 x 90 cm
  2. 1,8 … is ongeveer 180 cm
  3. 1,8 m = 180 cm
Je kunt ook die 90 cm meteen in gedachten vervangen door 1 m.
Je ziet dan meteen dat de hoogte 1,8 meter moet zijn.
cito oefenen groep 8
  1. tuin is 10 m x 16 m
    hoeveel tegels van 2 m x 2 m passen in de tuin?
  2. 10 x 16 m2 : 2 x 2 m2
  3. 10 x 16 : 2 x 2 = 160 : 4 = 40
Langs 10 meter kun je in gedachten 5 tegels leggen.
Langs 16 meter kun je in gedachten 8 tegels leggen.
5 x 8 = 40
cito oefenen
  1. 6 dL
    per dag 3 x 4 cL = 12 cL
    Hoeveel dagen?
  2. 6 dL : 12 cL
  3. 6 dL : 12 cL = 60 cL : 12 cL = 5
cito oefenen groep 8
  1. tuin: 10 m x 15 m
    500 gram zaad voor 100 m2
    100 gram zaad kost 12€
    Hoeveel kost zaad voor de hele tuin?
  2. opp. tuin: 150 m2

    500 gram zaad voor 100 m2
    … gram zaad voor 150 m2

    100 gram zaad kost 12 euro
    … gram zaad kost … euro

  3. 500 gram zaad voor 100 m2
    250 gram zaad voor 50 m2
    750 gram zaad voor 150 m2

    100 gram zaad kost 12 euro
    750 gram zaad kost 7,5 x 12 = 90 €
cito
  1. badkamer is 5 m x 2,5 m
    tegels zijn 50 cm x 50 cm
    Hoeveel tegels nodig?
  2. opp. badkamer: 5 x 2,5 m2
    opp. tegel: 50 x 50 cm2
    opp. badkamer : opp. tegel
  3. 5 x 2,5 m2 = 12,5 m2
    50 x 50 cm2 = 0,5 x 0,5 m2 = 0,25 m2
    12,5 : 0,25 = 1250 : 25 = 50
Langs 5 meter passen 10 tegels van 1/2 meter.
Langs 2,5 meter passen 5 tegels van 1/2 meter.
10 x 5 = 50
cito
  1. tuin is 5 m x 6 m
    aarde 10 cm x 5 m x 6 m
    zak aarde is 40 L
    Hoeveel zakken aarde?
  2. inhoud laag aarde: 0,1 x 5 x 6 m3
    zak aarde is 40 L
    Hoeveel zakken aarde?
  3. inhoud laag aarde:
    0,1 x 5 x 6 m3 = 3 m3

    3 m3 : 40 L =
    3 000 dm3 : 40 L =
    3 000 L : 40 L =
    300 : 4 =
    75

premium breuken

Geef een reactie

  1. Een half, een derde en een kwart

    ( khan-exercise file: EenHalfEenDerdeEnEenKwart.html )


    16-4-2013 11-30-49

  2. Een breuk op de getallenlijn zetten

    ( khan-exercise file: NieuweGetallenOpDeGetallenlijn.html )


    16-4-2013 11-30-49

  3. Twee vijfde

    ( khan-exercise file: BreukenOpDeGetallenlijn.html )


    16-4-2013 11-30-49

  4. Teller en noemer

    ( khan-exercise file: TellerEnNoemer.html )


    16-4-2013 11-30-49

  5. Een breuk anders opschrijven

    ( khan-exercise file: TellerEnNoemerDelenDoorGemeenschappelijkeFactor.html )


    16-4-2013 11-30-49

Cito vragen over verhoudingen

Geef een reactie
.
cito oefenen groep-7-8-plaatje Bij deze paragraaf hoort het leerwerkboek: Toets voorbereiding voor groep 7 en 8.
De Cito-score kan fors omhoog door dit doelgerichte oefenboek met antwoordenboek.

Bekijk de verkrijgbare titels op de winkelsite.
wiskunde piramide In dit leerwerkboek worden de eerste zes bouwlagen van de wiskunde-piramide behandeld.

Het rekenonderwijs/wiskundeonderwijs is opgebouwd als een piramide: elke laag bouwstenen wordt zorgvuldig op de vorige gelegd; je kunt geen laagje missen.

Slechts één slechte leer-periode kan er de oorzaak van zijn dat een leerling een reken-bouwlaag mist waardoor hij of zij misschien zelfs nooit meer iets van wiskunde zal begrijpen.

Met deze leerwerkboeken worden hiaten in kennis voorkomen.
Ook kunnen ontbrekende kennislagen achteraf worden opgevuld.

Klik hier voor meer informatie over het belang van een leerwerkboek.

Uitleg video, een soort citotrainer over verhoudingen

Uitleg samenvatting

In het witte en gele kader volg je de normale procedure.
In het lichter blauwe kader reken je vanaf de antwoorden.
In het donker blauwe kader zie je hoe je de vraag zonder echt te rekenen kunt beantwoorden.

citotrainer groep 8
  1. 750 op de 1750 vrouwen
  2. 750 : 1750 = …
  3. 750 : 1750 = 75 : 175 = 3 : 7

    (teller en noemer delen door 10 en daarna nog door 25)

    Bekijk zo nodig eerst de paragraaf over het vereenvoudigen van een verhouding.

Je ziet in één oogopslag dat C niet goed kan zijn want 1750 is niet twee keer meer dan 750.
Antwoord A is in feite hetzelfde als C en kan dus ook niet goed zijn.
Kiezen tussen B en D is moeilijker maar de antwoorden suggereren wel dat je 750 moet zien te veranderen in 3. Dat betekent delen door 250.
Je moet kiezen tussen B en D want A en C zijn duidelijk onjuist.
3 : 7 of 3 : 8? Je ziet dat 1750 niet deelbaar is door 8 (je kunt het maar één keer door twee delen), dus kies je 3 : 7.
citotrainer groep 8
  1. In de keuze-antwoorden zie je steeds ‘ongeveer’ staan.
    Dit moet je even in gedachten houden.
    304 op de 400 mensen
  2. 300 : 400 = …
  3. 300 : 400 = 3 : 4

    (teller en noemer delen door 100)

    Bekijk zo nodig eerst de paragraaf over het vereenvoudigen van een verhouding.

Antwoord B is duidelijk niet juist. Ook antwoord C kun je gelijk doorstrepen.
Je kunt meteen gokken op antwoord D omdat dat antwoord ook een 3 en een 4 bevat.
citotrainer groep 8
  1. 60 blanco voor €90
    60 ruitjes voor €30
    40 blanco voor … + 20 ruitjes voor …
  2. 60 blanco voor €90
    40 blanco voor …

    60 ruitjes voor €30
    20 ruitjes voor …

    optellen

  3. 60 blanco voor €90
    20 blanco voor €30
    40 blanco voor €60

    60 ruitjes voor €30
    20 ruitjes voor €10

    60 + 10 = 70

Ze kopen alle drie 60 schriften. De blanco schriften zijn drie keer duurder.
Petra koopt 40 blanco schriften en 20 goedkopere schriften. Zij moet daarom iets minder dan €90 betalen. 70 euro lijkt daarom wel goed.
citotrainer groep 8
  1. \text{100 pond} \approx \text{125 euro}
    \text{40 pond} \approx \text{... euro}
  2. 100 pond = 125 euro
    4 pond = 5 euro
    40 pond = 50 euro
B klopt niet omdat een pond dan gelijk zou zijn aan een euro.
C en D kloppen niet omdat ze veel te hoog zijn, bijna twee keer duurder.
B klopt niet omdat een pond dan gelijk zou zijn aan een euro.
C en D kloppen niet omdat ze veel te hoog zijn, bijna twee keer duurder.
citotrainer groep 8
  1. 12,5% heeft een hond.
    Welk deel heeft geen hond?
  2. \frac{1}{8}\text{ heeft een hond}
    \frac{7}{8}\text{ heeft geen hond}

    \frac{7}{8} = ... : ...

  3. \frac{7}{8}\text{ = 7 op de 8 = 70 op de 80}
B klopt zeker niet.

Cito vragen over procenten

Geef een reactie
.
cito oefenen groep-7-8-plaatje Bij deze paragraaf hoort het leerwerkboek: Toets voorbereiding voor groep 7 en 8.
De Cito-score kan fors omhoog door dit doelgerichte oefenboek met antwoordenboek.

Bekijk de verkrijgbare titels op de winkelsite.
wiskunde piramide In dit leerwerkboek worden de eerste zes bouwlagen van de wiskunde-piramide behandeld.

Het rekenonderwijs/wiskundeonderwijs is opgebouwd als een piramide: elke laag bouwstenen wordt zorgvuldig op de vorige gelegd; je kunt geen laagje missen.

Slechts één slechte leer-periode kan er de oorzaak van zijn dat een leerling een reken-bouwlaag mist waardoor hij of zij misschien zelfs nooit meer iets van wiskunde zal begrijpen.

Met deze leerwerkboeken worden hiaten in kennis voorkomen.
Ook kunnen ontbrekende kennislagen achteraf worden opgevuld.

Klik hier voor meer informatie over het belang van een leerwerkboek.

Cito Eindtoets rekenvragen over procenten: uitleg video

Cito eindtoets, vragen over procenten: samenvatting

In het witte en gele kader volg je de normale procedure.
In het lichter blauwe kader reken je vanaf de antwoorden.
In het donker blauwe kader zie je hoe je de vraag zonder echt te rekenen kunt beantwoorden.
cito groep 8
  1. 3,5% vet in de melk. Welk deel?
    De rest heb je niet nodig, het plaatje geeft geen extra informatie
  2. 3,5 % = … deel
  3. 3,5\% = \frac{3,5}{100} = \frac{7}{200}

    Bij de laatste stap heb je de teller en de noemer van de breuk allebei met 2 vermenigvuldigd.
    Dat mag want de waarde van de breuk verandert daardoor niet.
    Zie zo nodig Breuken 10 – De noemer groter maken.

  4. Omdat je dit vreemde antwoord erbij ziet, kun je het hier ook bij laten en gewoon nog even je berekening doorlopen.

    \[\frac{1}{3} = 33,3..\%\]

    \[\frac{1}{5} = 20\%\]

    \[\frac{3}{10} = 30\%\]

    \[\frac{7}{200} = \frac{3,5}{100} = 3,5\%\]

3,5% is een heel klein deel.
De antwoorden A, B en C zijn veel te groot.
cito Eindtoets groep 8
  1. Zonder korting betaalt hij €500.
    Hij krijgt wel 20% korting want hij boekt op tijd.
    Hij betaalt dus 80% van de prijs.
  2. 80% van 500
  3. 1% = 5
    80% = 80 x 5 = 400
20% korting, ofwel 1/5 deel korting.
B, C en D lijken wel erg laag.
cito Eindtoets groep 8
  2. 66 = …% van 120
  3. 1% = 1,2
    66 : 1,2 = 55
1% = 1,2
22% = 22 x 1,2 < 66
5,5% = 5,5 x 1,2 < 66
55% = 55 x 1,2 = 66
66 is iets meer dan de helft van 120.
Het antwoord moet dus iets meer zijn dan 50 (procent).
Nu nog kiezen tussen C en D.
C lijkt goed omdat D maar een héél klein beetje groter is dan 50.
cito toets
  1. 79% is man, dan is 21% vrouw.
    Dus ongeveer 20% is vrouw.
  2. 20% = … deel
  3. 20\% = \frac{20}{100} = \frac{1}{5} = 1 : 5
1 op de 4 = 1/4 = 25/100 = 25%
1 op de 5 = 1/5 = 20/100 = 20%
cito toets
  1. Je had eerst 20 rode hokjes. Daarna heb je nog 5 hokjes er bij gekocht.
  2. 5 is … % van 20
  3. 5 is een vierde deel van 20.
    Een vierde deel is hetzelfde als 25%.
25% van 20 = 1/4 x 20 = 5 blauwe hokjes
50% is al veel te groot, dus antwoord A
cito toets
  1. Klaasje betaalt in euro: 30 x 35
    Kay betaalt in euro: 30 x 40 met 25 % korting
    Hoeveel betaalt Kay minder?
  2. 30 x 35
    min
    30 x 40 met 25% korting
  3. Kay betaalt niet 40 euro maar 30 euro per m2.

    30 x 35
    min
    30 x 30

    1050 – 900 = 150

De een betaalt 35 euro, de ander 30 euro per vierkante meter.
Het verschil is 5 euro. 5 x 30 = 150.
cito toets groep 8
  1. \text{2400 boten}
    12\frac{1}{2}\5\% \text{ is zeilboot}
  2. 12\frac{1}{2}\5\% \text{ van } 2400 = ...
  3. 12\frac{1}{2}\5\% \text{ van } 2400 =
    \frac{1}{8} \text{deel van 2400} =
    2400 : 8 = 300
Je kunt het ook veel ruwer schatten. Meer dan 10% van 2400 is meer dan 240, dus 300 zal wel goed zijn.
cito toets groep 8
  1. 2011:     1/2 blokje hoog

    2012:     2 blokjes hoog
            (1/2 + 300% van 1/2)

    2013:     … blokjes hoog
            (2 + 100% van 2)

  2. 2 + 100% van 2
  3. 2 + 100% van 2 =
    2 + 2 = 4
De omzet is gestegen dus je moet kiezen tussen A en B.

Lengtematen 5 – Omtrek

Omtrek: uitleg video

Omtrek berekenen: oefenen met werkbladen en/of met leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§8 van het leerwerkboek)
8_1
8_2
8_3
8_4
8_5

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §8 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Definitie van omtrek: online oefenen

1. Oefenen met de definitie van de omtrek

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


omlijning figuur berekenen

Berekenen omtrek rechthoek via zijde of omgekeerd: online oefenen

2. Oefenen met het berekenen van de omtrek of zijde van een rechthoek of vierkant

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


omlijning figuur berekenen

Berekenen omtrek rechthoek waarbij de zijden met verschillende lentematen zijn aangegeven: online oefenen

3. De omtrek van een rechthoek berekenen waarbij de eenheden van de zijden verschillen

Bij elke vraag kun je de oplossing stap voor stap bekijken.
Bij elke stap krijg je uitleg.
Hier onder zie je een voorbeeldsom.
Door er op te klikken wordt een nieuw window geopend met de oefening.


omlijning figuur berekenen

Omtrek, definitie en berekeningen: samenvatting

tegelvloer
Je ziet hier een blauwe rechthoek met daar omheen een soort lijst van touw. Om de lijst te maken heb je 22cm touw nodig. De omtrek van de blauwe rechthoek is 22cm.De omtrek van een rechthoek bereken je door de lengte van de lijntjes rondom de rechthoek bij elkaar op te tellen.
Bij een rechthoek van 7cm bij 4cm is de omtrek dus:
7cm + 4cm + 7cm + 4cm = 22 cm

vierkante-meter
Hier zie je een aantal andere figuren. De omtrek van een blauw vorm is gelijk aan de totale lengte van de bruine lijntjes rondom die vorm.