Categoriearchief: hele-getallen

Delen met hele getallen-post

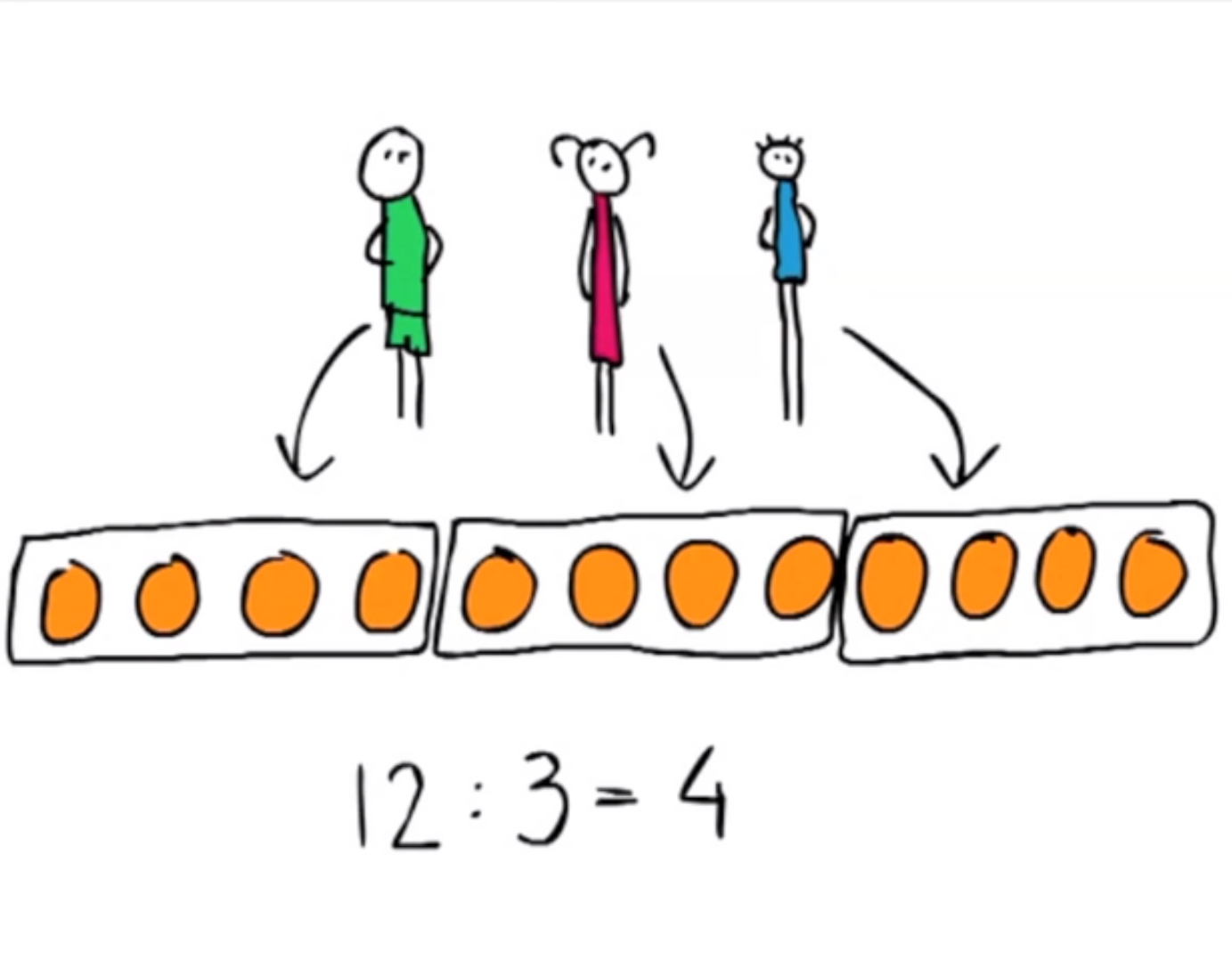
	1 – Wat is delen? Uitleg over de betekenis van delen. Voorbeelden waarbij een aantal voorwerpen verdeeld wordt onder een aantal kinderen. Uitleg filmpje Interactieve werkbladen met antwoordbladen
	2 – Delen en vermenigvuldigen horen bij elkaar Uitleg over het feit dat delen de omgekeerde bewerking is van vermenigvuldigen. Dit geeft ook de mogelijkheid om de uitkomst van een deling te controleren met een vermenigvuldiging. Uitleg filmpje Interactieve werkbladen met antwoordbladen
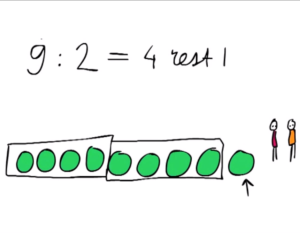	3 – Delen met rest Als je bijvoorbeeld 9 aardbeien wilt verdelen onder twee kinderen, blijft er één aardbei over. Die ene aardbei is ‘de rest’ die overblijft na de verdeling. Uitleg filmpje Interactieve werkbladen met antwoordbladen
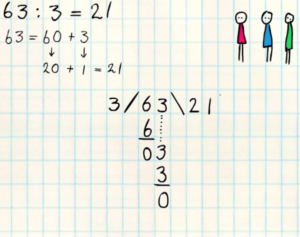	4 – Een staartdeling maken Hier worden een aantal zeer eenvoudige staartdelingen voorgedaan. Door de eenvoudig gekozen getallen wordt het duidelijk waarom zo’n staartdeling tot het goede antwoord leidt en waarom een staartdeling de handigste manier is voor het oplossen van een deelsom. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Een huiswerksom intypen en stap voor stap laten uitleggen
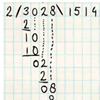	5 – Eenvoudige staartdeling zonder rest Hier worden nog een paar eenvoudige staartdelingen voorgedaan, nu wel met af en toe een ’tussen-rest’. Door de eenvoudig gekozen getallen wordt nogmaals duidelijk waarom zo’n staartdeling tot het goede antwoord leidt en waarom een staartdeling de handigste manier is voor het oplossen van een deelsom. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Een huiswerksom intypen en stap voor stap laten uitleggen
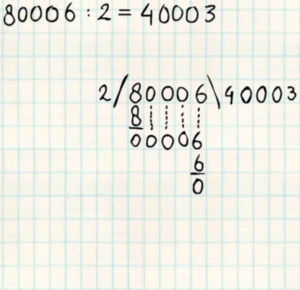	6 – Staartdeling met nullen in het antwoord Het aanhalen van nullen lijkt in het begin moeilijk maar is in feite zeer eenvoudig. Door de uitleg blijkt ook nu heel duidelijk waarom de staartdeling altijd snel en effectief tot het goede antwoord leidt. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Een huiswerksom intypen en stap voor stap laten uitleggen
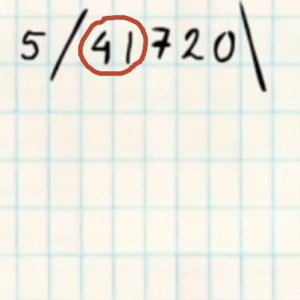	7 – Iets moeilijker staartdeling Soms moet je bij het begin van een staartdeling niet alleen naar het eerste cijfer van het deelgetal kijken maar naar de eerste twee cijfers. Dit is heel begrijpelijk maar het is even wennen in het begin. Na een paar keer oefenen is ook dit soort staartdeling heel eenvoudig zelf te maken. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Een huiswerksom intypen en stap voor stap laten uitleggen
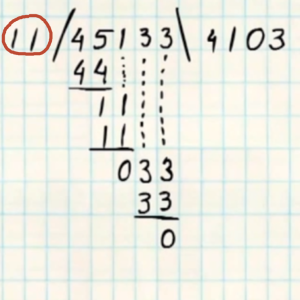	8 – Staartdeling met deler groter dan 10 Als de deler groter is dan tien, gaat de staartdeling in feite toch op precies dezelfde manier. Het is alleen even wennen en een paar keer goed oefenen. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Een huiswerksom intypen en stap voor stap laten uitleggen
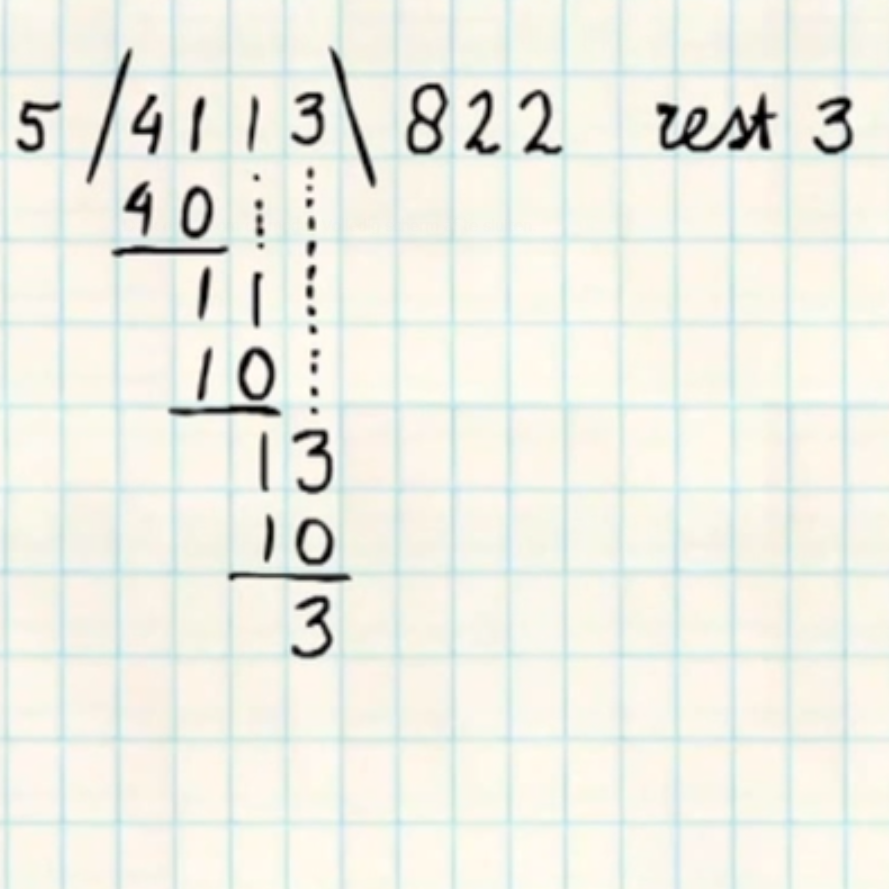	9 – Staartdeling met rest Soms staat er aan het eind van een staartdeling geen nul maar een groter getal. Dit getal noemen we de ‘rest’. In het eerste filmpje is al uitgelegd dan er soms iets over blijft als je bijvoorbeeld een aantal aardbeien onder een aantal kinderen verdeelt. De staartdeling wordt er niet moeilijker door. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Een huiswerksom intypen en stap voor stap laten uitleggen

Vermenigvuldigen met hele getallen-post

Geef een reactie

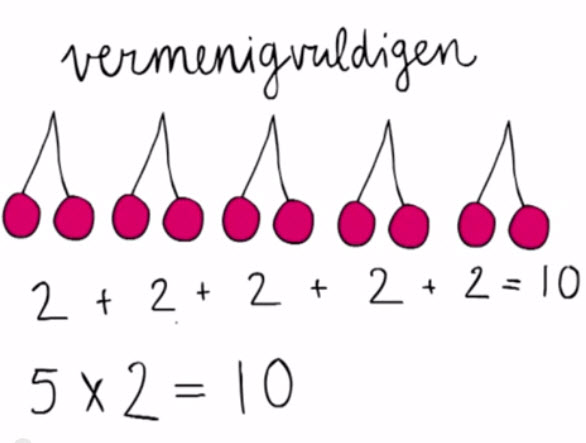	1 – Wat is vermenigvuldigen? Voorbeelden van herhaald optellen met groepjes kersen, ijsbolletjes en meer. Uitleg filmpje
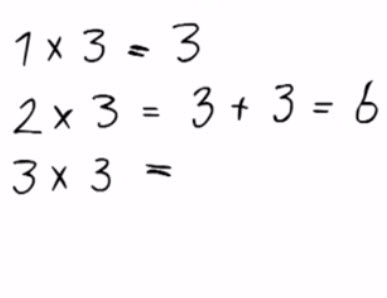	2 – Vermenigvuldigen onder de tien (de tafels van vermenigvuldiging) Uitleg van de tafels. Bij de werkbladen kan men bijvoorbeeld zelf instellen: 100 vragen over de tien tafels (standaard instelling) 25 vragen over de tafel van 7 50 vragen over de tafels van 3 en 5 … Uitleg filmpje Interactieve werkbladen met antwoordbladen
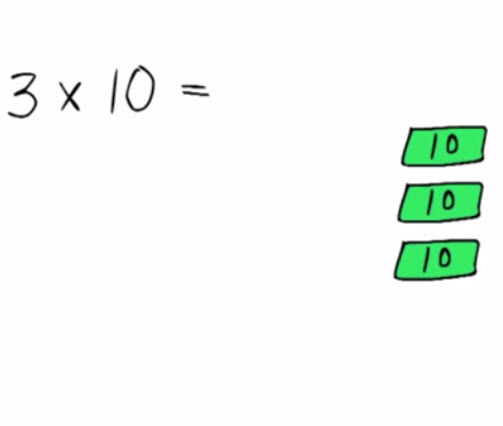	3 – Vermenigvuldigen met 10, 100, 1000, enz. Het is erg belangrijk om meteen te weten hoeveel 3 maal 10 is of 5 maal 1000. Bovendien is het zeer eenvoudig. In de video wordt duidelijk gemaakt waarom ‘maal tien’ niet moeilijker is dan gewoon een nul achter een getal zetten. En dat ‘maal honderd’ twee nullen meer toevoegt achter een getal. Veel oefenen verhoogt het inzicht in het tientallig stelsel. Ook is van belang voor het goed kunnen schatten van de orde van grootte van een antwoord. Uitleg filmpje Interactieve werkbladen met antwoordbladen
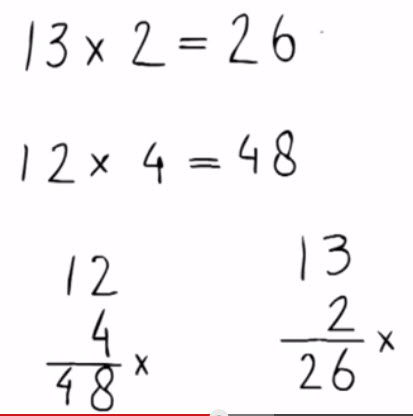	4 – Vermenigvuldigen onder elkaar zonder onthouden Het antwoord op elke vermenigvuldiging kan foutloos en exact worden berekend door de standaardprocedure van het vermenigvuldigen onder elkaar. Het is niet moeilijk om te begrijpen waarom deze methode altijd werkt. Het uitlegfilmpje laat dit zien. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Huiswerksom intypen en laten uitleggen
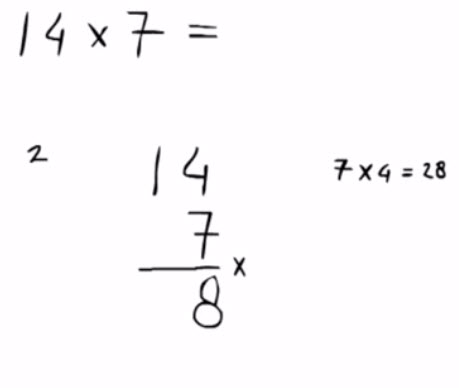	5 – Vermenigvuldigen met onthouden, onder de honderd Vaak krijg je bij het werken onder elkaar een tussen-antwoord van twee cijfers. Je moet dan alleen het tweede cijfer opschrijven en het eerste cijfer even onthouden. Het hoe en waarom wordt in de video uitgelegd. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Huiswerksom intypen en laten uitleggen
	6 – Vermenigvuldigen met onthouden, met een groot getal Een getal onder de tien maal een getal van drie cijfers of meer, werkt op precies dezelfde manier en is niet moeilijker. Regelmatig wat oefenen maakt dat elke vermenigvuldiging eenvoudig wordt en altijd tot het goede en exacte antwoord leidt. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Huiswerksom intypen en laten uitleggen
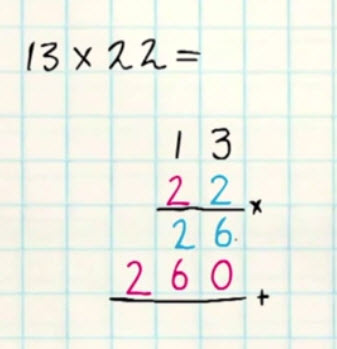	7 – Vermenigvuldigen zonder onthouden van twee getallen boven de tien Bij de vermenigvuldiging van twee grotere getallen zijn meerdere regels nodig maar het is in principe niet echt moeilijker. In het uitlegfilmpje wordt duidelijk gemaakt hoe de standaard procedure werkt en waarom het altijd het goede antwoord geeft. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Huiswerksom intypen en laten uitleggen
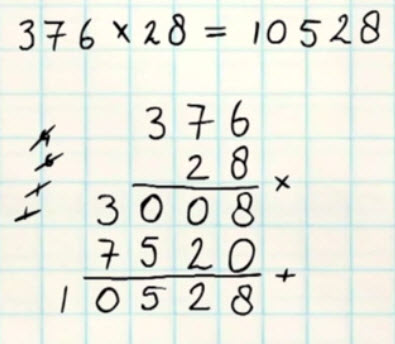	8 – Vermenigvuldigen met onthouden van twee getallen boven de tien Ook bij het product van twee grotere getallen moet je natuurlijk soms even een cijfer ‘onthouden’. Als deze sommetjes met behulp van de werkbladen goed worden geoefend, is geen enkele vermenigvuldiging meer te moeilijk. Elke vermenigvuldiging kan je nu zonder problemen en foutloos uitrekenen! Uitleg filmpje Oefenen op de computer Interactieve werkbladen met uitgewerkte antwoordbladen Huiswerksom intypen en laten uitleggen

Aftrekken met hele getallen-post

Geef een reactie

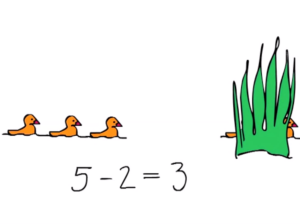	1 – Aftrekken onder de tien Wat is aftrekken? Ook aandacht voor het min-teken. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met antwoordbladen
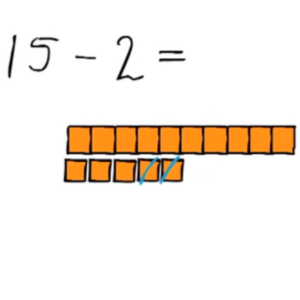	2 – Aftrekken onder de twintig Sommetjes zoals 15-5, 15-2, 17-6, enz. Het antwoord komt niet onder de tien. Uitleg filmpje
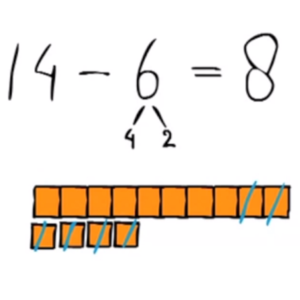	3 – Aftrekken onder de twintig met ‘splitsen’ Bij 17 – 9 kun je het 9 splitsen in een 7 plus een 2. Dit splitsen wordt na verloop van tijd automatisch gedaan zonder dat het expliciet wordt opgeschreven. Uitleg filmpje Interactieve werkbladen met antwoordbladen
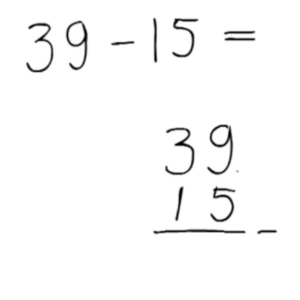	4 – Aftrekken onder elkaar zonder ‘lenen’ Als je weet hoe je de getallen onder elkaar schrijft en als je het optellen onder elkaar begrijpt, is dit type aftreksom zeer eenvoudig. Dit komt ook omdat er nog niet hoeft te worden ‘geleend’. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom intypen en laten uitleggen
	5 – Aftrekken onder elkaar met één keer ‘lenen’ Het ‘lenen’ is de grote moeilijkheid bij het aftrekken maar als dit eenmaal met geld is uitgelegd, wordt ook dit type som zeer eenvoudig. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom intypen en laten uitleggen
	6 – Aftrekken onder elkaar met meerdere keren ‘lenen’ Als het één keer lenen goed is geoefend met werkbladen, dan is het meerdere keren lenen niet echt moeilijk meer. De procedure verschilt niet en door de uitleg met geld is dit alles ook zeer begrijpelijk. Veel oefenen, vooral m.b.v. werkbladen, geeft steeds meer inzicht in het tientallig stelsel. Ook wordt steeds duidelijker waarom het optellen en het aftrekken onder elkaar het meest handig is en altijd leidt naar het goede antwoord. Welke getallen je ook kiest bij de vraagstelling. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom intypen en laten uitleggen
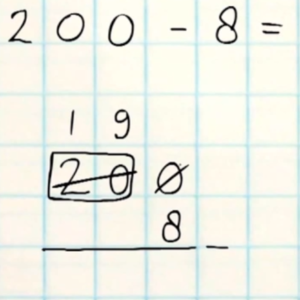	7 – Aftrekken onder elkaar met meerdere keren ‘lenen’ van nullen Het ‘lenen van een nul’ lijkt vreemd maar is in feite niets nieuws. Wel moet hier goed in geoefend worden om te wennen aan het lenen van nullen, zeker als er meerdere nullen achter elkaar staan in het eerste getal. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom intypen en laten uitleggen

Optellen met hele getallen-post

Geef een reactie

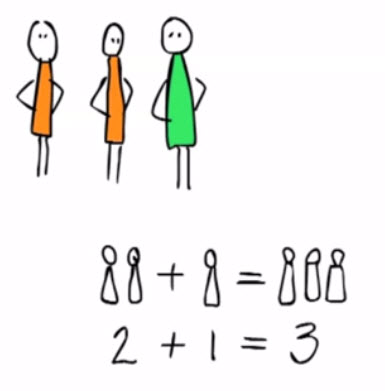	1 – Optellen onder het tiental Uitleg over de betekenis van optellen. Uitleg over het plus-teken en het is-teken. Bij een tweede uitlegfilmpje uitleg over wat een getallenlijn is en hoe je een zeer eenvoudig optelsommetje op de getallenlijn kunt uitrekenen. Twee uitleg filmpjes Oefenen op de computer Interactieve werkbladen met antwoordbladen
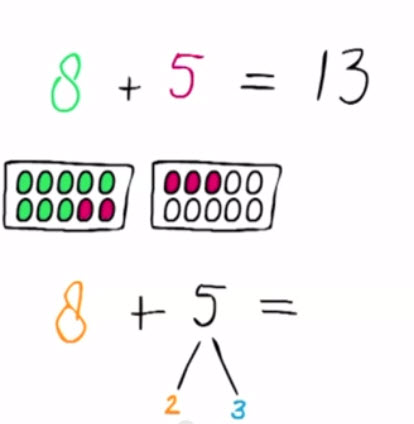	2 – Optellen over het tiental Uitleg over paren van tien. Een tweede uitlegfilmpje gaat over het opsplitsen van een getal zodat een paar van tien ontstaat in de optelsom. Twee uitleg filmpjes Oefenen op de computer Interactieve werkbladen met antwoordbladen
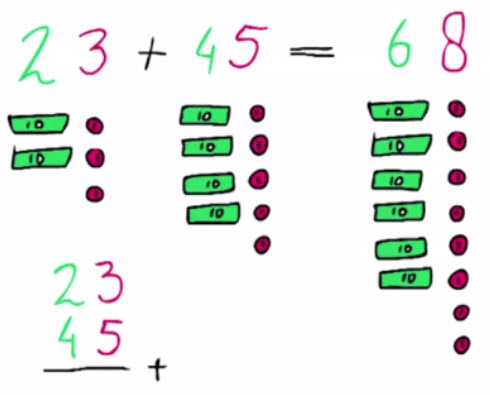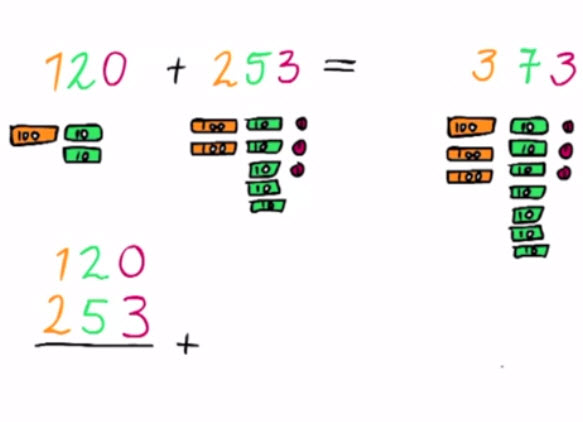	3 – Optellen onder de honderd zonder onthouden Hier wordt het optellen onder elkaar geïntroduceerd. Later zal duidelijk worden waarom dit de handigste methode van optellen is waarmee elke optelsom foutloos kan worden uitgerekend. Uitleg filmpje Oefenen op de computer Interactieve werkbladen met antwoordbladen Zelf een huiswerksom intypen en laten uitleggen
	4 – Optellen boven de honderd zonder onthouden Bij het optellen onder elkaar doe je niets anders dan eerst de eenheden (de euromunten) bij elkaar op te tellen, dan de tientjes bij elkaar te nemen, dan de honderdjes, dan de duizendjes, enz. Later zal duidelijk worden waarom je altijd bij de eenheden (munten) begint en dus van rechts naar links optelt. Utleg Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom laten uitleggen
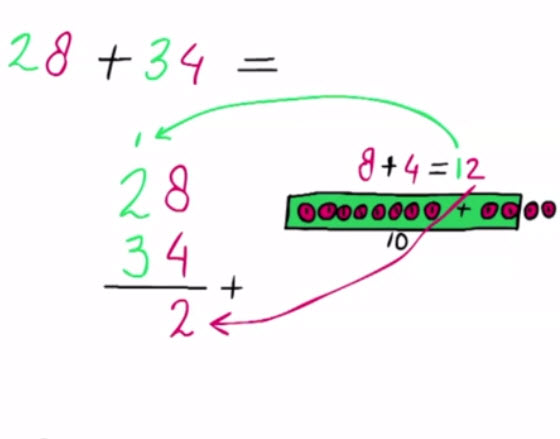	5 – Optellen onder de honderd met onthouden Nu wordt duidelijk waarom je bij het optellen begint bij de eenheden en vervolgens de tientallen, honderdtallen, enz . bij elkaar neemt. Als je in totaal twaalf losse euromunten hebt, kun je tien van die munten inwisselen voor een tientje. Dit tientje komt dan bij het totaal van het aantal tientjes. Je moet het tientje ‘onthouden’. Daarom tel je de tientallen pas op nadat je eerst de eenheden hebt opgeteld. Utleg Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom laten uitleggen
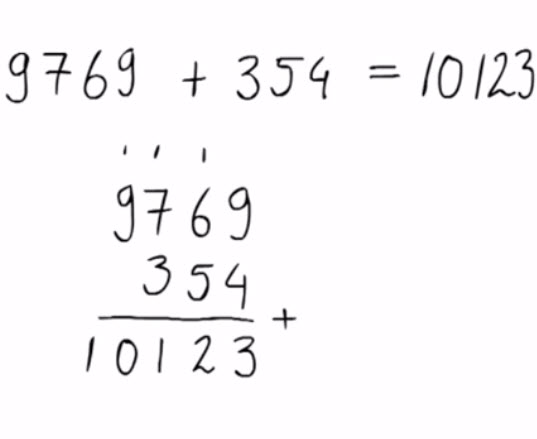	6 – Optellen met meerdere keren onthouden Soms kun je tien losse euromunten inwisselen voor een tientje en daarna ook nog tien tientjes inwisselen voor een honderdje. Utleg Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom laten uitleggen
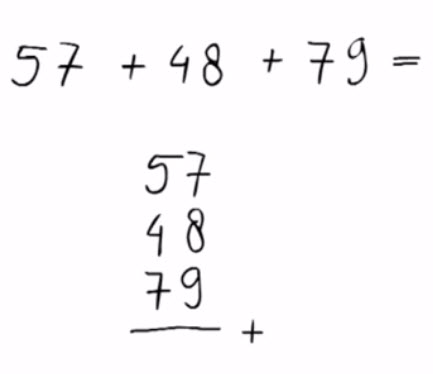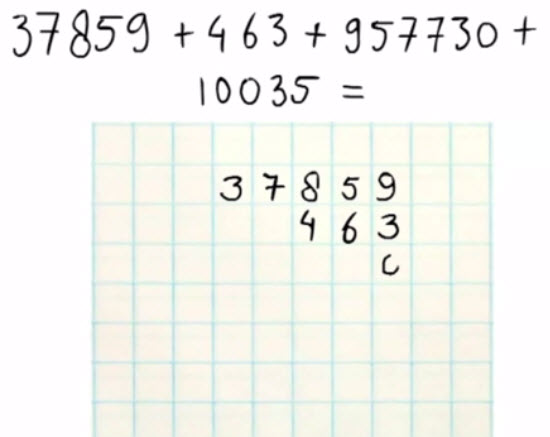	7 – Optellen van meerdere getallen met onthouden Het optellen van drie getallen is nu zeer eenvoudig. Het werkt op precies dezelfde manier als het optellen van twee getallen. Met de standaardprocedure van het optellen onder elkaar kan elke som zonder problemen worden opgelost. Door veel te oefenen krijgt de leerling vanzelf een zeer goed begrip van het tientallig stelsel. Hij gaat begrijpen waarom het een zeer handig getalstelsel is waarom je bij optellen begint bij de eenheden en van rechts naar links werkt waarbij af en toe een cijfer moet worden toegevoegd aan een kolom die zich één plaats naar links bevindt. Utleg Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom laten uitleggen
	8 – Optelsommen onder elkaar schrijven met ruitjespapier Netjes werken op ruitjespapier is belangrijk. Elke optelsom wordt dan eenvoudig, hoe moeilijk hij er ook uitziet. Dit onderdeel kan ook eerder worden bekeken, bijvoorbeeld na de paragraaf ‘Optellen 2’. Utleg Oefenen op de computer Interactieve werkbladen met antwoordbladen Huiswerksom laten uitleggen

Optellen 8 – Optelsommen onder elkaar schrijven met ruitjespapier

Uitleg over het optellen onder elkaar, hoe je dat foutloos doet met ruitjespapier. Je kunt nu alle optelsommen met willekeurige hele getallen foutloos uitrekenen.

Blijven oefenen met het optellen van meerdere willekeurige hele getallen: oefenen met de herhalingsopgaven uit het leerwerkboek

Je kunt zorgen dat je de stof niet vergeet als je blijft oefenen met de herhalingsopgaven over optellen uit het leerwerkboek over het rekenen met hele getallen voor groep 5, groep 6, groep 7 en groep 8.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

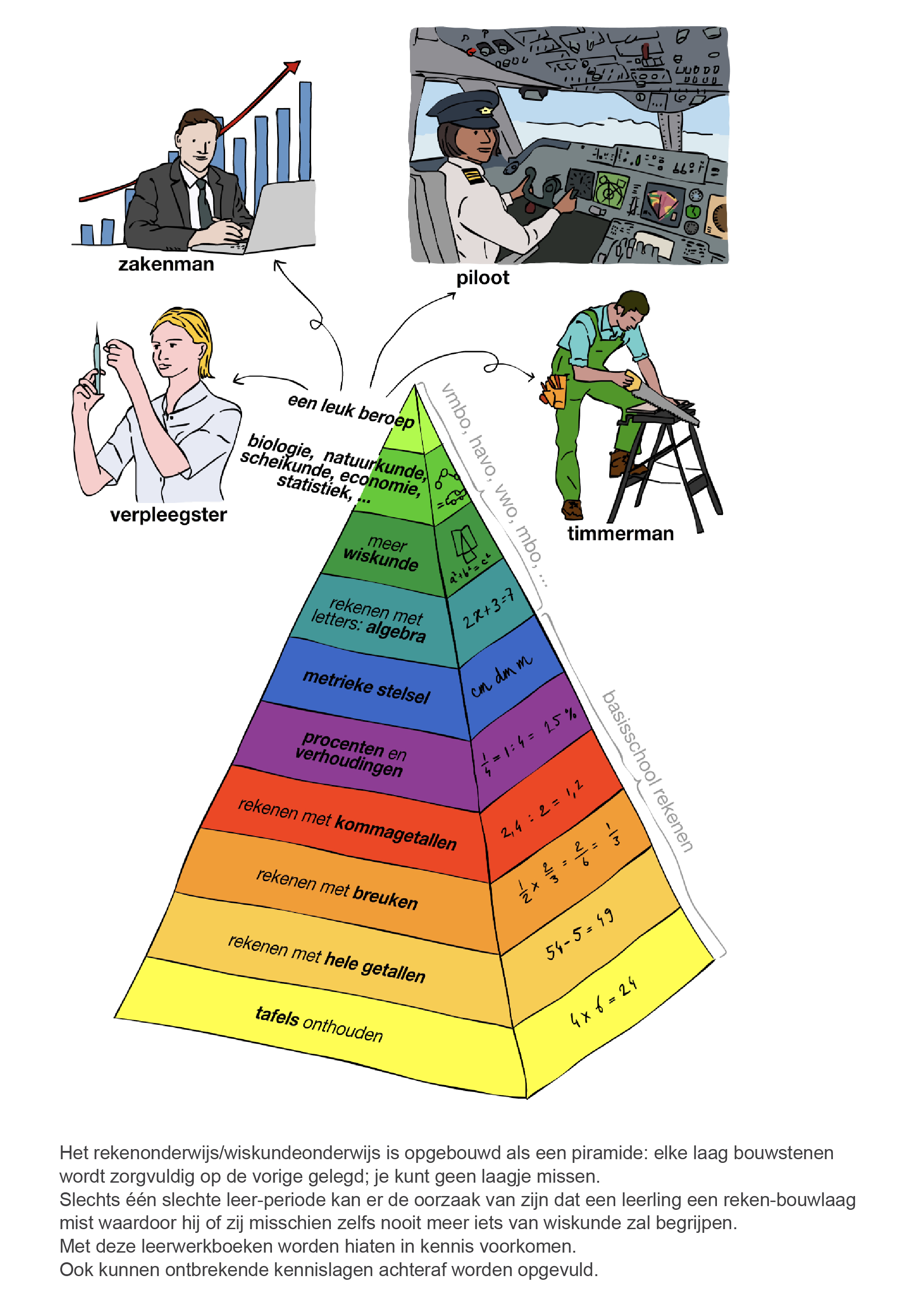
Wiskunde is een piramide

Het wiskundeonderwijs is opgebouwd als een piramide: elke laag bouwstenen wordt zorgvuldig op de vorige gelegd; je kunt geen laagje missen.
Slechts één slechte leer-periode kan er de oorzaak van zijn dat je een reken-bouwlaag mist waardoor je misschien zelfs nooit meer iets van wiskunde kunt begrijpen.
Met deze site en met de leerwerkboeken worden hiaten in kennis voorkomen.
Klik hier voor meer informatie over het belang van een leerwerkboek.
Bekijk de verkrijgbare titels op de winkelsite.

Optellen 7 – Optellen van meerdere getallen met onthouden

Uitleg video optellen groep 5

Oefenen met optellen met meerdere keren onthouden: oefenen met extra werkbladen of met leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§4 van het leerwerkboek)
4_1
4_2
4_3
4_4
4_5

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §4 van het leerwerkboek voor groep 5, groep 6, groep 7 en groep 8.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Optellen 6 – Optellen met meerdere keren onthouden

Optellen met meerdere keren onthouden: video uitleg

Oefenen met optellen met meerdere keren onthouden: oefenen met extra werkbladen of met leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§3 van het leerwerkboek)
3_1
3_2
3_3
3_4
3_5

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §3 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Optellen 5 – Optellen onder de honderd met onthouden

Uitleg video optellen groep 5, optellen onder de 100 met onthouden

Optellen onder de honderd met onthouden: oefenen met extra werkbladen of met leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§2 van het leerwerkboek)
2_1
2_2
2_3
2_4
2_5

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §2 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Optellen 4 – Optellen boven de honderd zonder onthouden

Optellen onder elkaar boven de 100 zonder onthouden: uitleg video

Oefenen met optellen boven de honderd zonder onthouden, met extra werkbladen of met leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§15 van het leerwerkboek)
15_1
15_2
15_3
15_4
15_5

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §15 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.

Aftrekken 7 – Aftrekken onder elkaar met meerdere keren ‘lenen’ van nullen

Minsommen met meerdere keren lenen, uitleg video, oefenen met werkblad met uitgewerkt antwoordblad en/of met leerwerkboek.

Aftreksommen met lenen: uitleg video

Oefenen met aftrekken onder elkaar met meerdere keren lenen: oefenen met extra werkbladen of met leerwerkboek

Oefen direct met de uitgelegde stof. Dit kan met de losse werkbladen en antwoordbladen die horen bij deze video (§7 van het leerwerkboek)
7_1
7_2
7_3
7_4
7_5

aftrekken groep 5, groep 6, groep 7 en groep 8

Je kunt de stof nog sneller onder de knie krijgen als je oefent met §7 van het leerwerkboek.
Je houdt daarmee het overzicht van de stof, ook voor later, via plaatjes van de stof en via de uitgelegde en door jou verbeterde antwoorden.